8下平行四边形证明题

缺条件,应先证明ABCD为平行四边形,如果不能证明,该题就是错的
怎样证明平行四边形
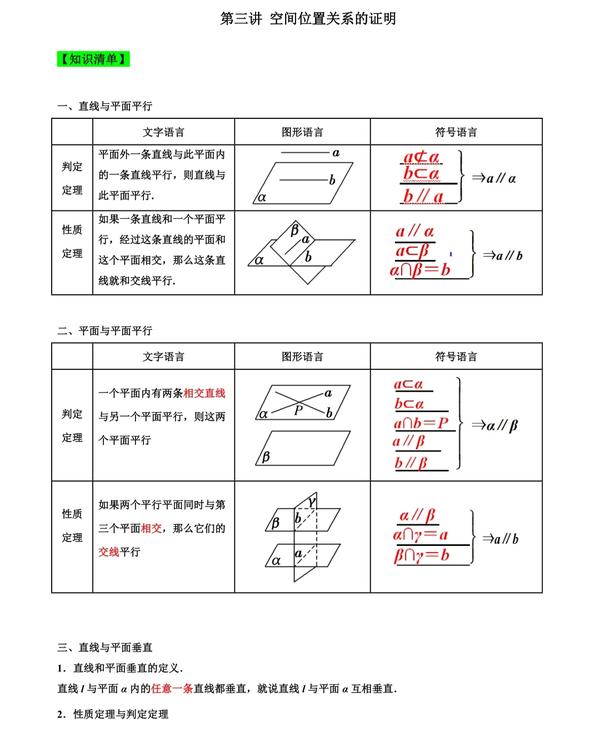
高一数学立体几何学习,平行与垂直关系的证明,平行关系的证明比较简单,考点主要是线面平行,对于线面平行的证明,两种方法,一种证明线面一种证明面面,而辅助线常考中位线定理或者平行四边形,或者是相似,注意找点问题,通常是中点或者三等分点。垂直关系的证明有三种,证线线垂直,线面垂直或者面面垂直,不管证明
中考必考,初中几何平行四边形知识点归纳总结,适合基础薄弱的学生,赶紧收藏。(之前分享过类似知识点,请翻以前记录)1.平行四边形的定义2.平行四边形的性质3.平行四边形的判定方法4.特殊平行四边形中的证明和计算.
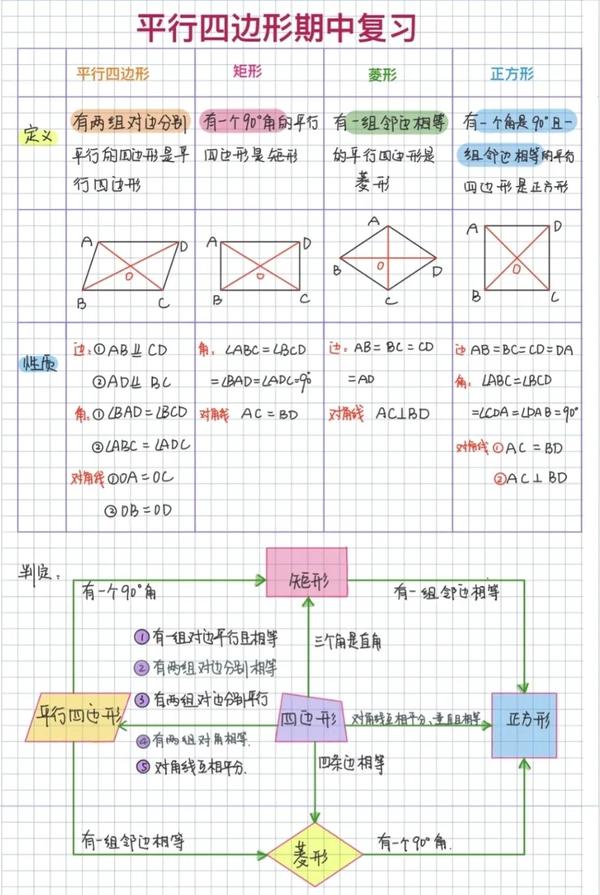
数学课上的一点力气没有,问根据菱形定义,怎么推出对角线互相垂直,学生说全等,我说不用全等怎么证?鸦雀无声。第二题我说怎么证明四边形ABDE是平行四边形?貌似都不知道对边平行。这…我是不是问多了
怎样证明平行四边形是菱形
空间图形的位置关系之平行关系。这个知识点的重难点不言而喻。常见的方法(1)有中点优先考虑中位线(2)证明平行四边形(3)证明面面平行。 欢迎大家评论+转发。创作不易,请点赞评论。
如果是面对小学生,我可能会这样解说这道题:参考平行四边形的面积公式的证明方法,把这个道路凸的部分割下来平移到凹的部分,最后形成的图形就是一个平行四边形。
平行四边形这个章节不但八下的几何重点,还在中考中发挥重要作用。平行四边形的性质是证明两条直线平行、线段相等及角相等的重要依据。平行四边形的面积及周长、对称性也常出现在中考题中,这类题有填空题、选择题、计算题和证明题。深刻理解和牢记多边形、平行四边形的性质和判定是关键和前提。
初一数学,平行四边形证明,一共5个判定方法。图形求面积,在初中有两个办法,直接法需要确定图形的形状,并且该图形可以用面积公式;间接法主要是割补法,割即是把图形分割为若干个我们熟悉的图形,补即是补上一部分将原图形变成我们熟悉的图形。
高一学生学到了立体几何,这个模块必须要去突破,如果学不好,到了高三多数学生难突破。解答题两问,第一问平行关系和垂直关系的证明,平行关系要利用中位线和平行四边形法则,或者相似证平行,或者证明面面平行。垂直关系都要经过线面垂直,但是垂直关系的证明相对平行关系会难,一般都需要去做转化,如果实在没有思路,把
