谈起整数,你一定会想:这不是小学就学过的概念吗?
整数不就是像-3,-2,0,1,2,3这样的数吗? 而且整数在生活中
处处皆是
,它对人们来说再熟悉不过了。 
可是看完今天的文章,你会发现,
当我们谈论“整数”时,我们在谈些什么?
为什么我们会用符号Z表示整数集呢?
这涉及到一个
德国女数学家
对环理论
的贡献,她叫诺特。 
早在1920年,诺特已经引入了数学中“左模”,“右模”的概念。1921年出版的《整环的理想理论》更是交换代数发展的
里程碑
。其中,诺特在引入整数环概念的时候,由于她是德国人,德语
中的整数叫做Zahlen
,于是她便将整数环记作Z,也就是从那时候起整数集就用Z表示了。中国最早引进了负数,但“0”却被印度人抢先注册
最早引进和使用负数是
《九章算术》
的一项突出的贡献。在《九章算术》
的“方程术”中,当用遍乘直除算法消元时,可能出现减数大于被减数的情形。为此,就需要引进负数。《九章算术》
在方程章中提出了组下的“正负术”:同名扫除,异名相益,正无入负之,负无入正之。 其异名相除,同名相益,正无入正之,负无入员之。
这实际上就是正负数和零的加减运算法。 
虽然中国最早引进了负数,但0确是由印度人最早引入。公元前2500年左右,印度最古老的文献
<吠陀>
中已有“0”这个符号
的应用,当时的0在印度表示空的位置。但中国古代的筹算数码中没有
“零”,遇到“零”就空一位
。比如“6708”
就可以表示为“┴ ╥ ”
。 
就算有整数0也不让用
大约1500年前,欧洲数学家们是不知道用“0”这个数字的。这时,罗马有一位学者从印度计数法中发现了“0”这个符号。他发现,有了“0”,
进行数学运算非常方便
,于是便把印度人使用“0”的方法向大家做了介绍。这件事不久就被罗马教皇知道了。教皇非常愤怒,他认为神圣的数是上帝创造
的
,在罗马上帝创造的数里没有“0”这个怪物
。并以亵渎神灵罪把那位学者抓了起来,对他施加了酷刑。就这样,整数“0”在欧洲迟迟未能“上市”
,这很大程度上也是现在世界最常用的是阿拉伯数字
而不是罗马数字的原因之一。 
所有正整数的和等于负十二分之一
是的,你没有看错,
正数的和竟然会等于负数
!是不是感觉自己的世界观彻底被颠覆。 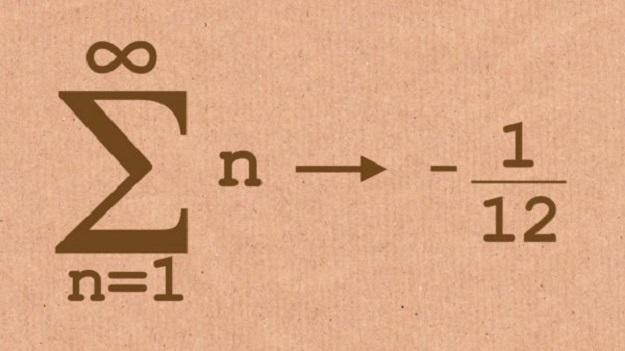
其实这个概念来源于国外的两期科学节目,其中一期介绍了
格兰迪级数
,另一期以此为基础推算出所有自然数之和等于-1/12
,论述过程十分缜密完备,有兴趣可以也可以在知乎上看到简易的推理过程。在数学上一旦涉及到“无穷”,很多公式甚至定义都有所限制了
,可以说“无穷”本身就是一个魔鬼!整数多了也会感到拥挤
在整数88,000,002,999 和 整数88,000,003,000之间,存在一个
新的整数
,虽然科学家们尚在探索这一片区域,但他们早已为这个整数取好了名字:“S
”。而接下来的这段话可能真的要让人Surprise
一下: 
如果数字“S”的存在得到确认,这将会使该区域内的计数问题更加复杂,因为为了使其存在有意义,
“S”很可能回向其两边的整数施加压力
。数学家们将这种压力称为“整数拥挤”
,并表示随着我们沿着数轴的正方向越走越远,该问题也将会变得越来越棘手
。